Parallelisierung durch Zerlegung
Anpassung von Finite-Elemente Simulationen auf Mehrkern-CPUs
Beitrag von Andreas Seibold B.Sc., Dipl.-Ing. Michael Leistner und Prof. Dr. Daniel Rixen, Lehrstuhl für Angewandte Mechanik, TU München
Numerische Verfahren, wie die Finite Elemente Methode, sind zur Berechnung ingenieurwissenschaftlicher Probleme kaum mehr wegzudenken. Die Verwendung von Mehrkern-CPUs und großen Hochleistungsrechnern stellt Forscher der TU München jedoch vor neue Herausforderungen. Mehr dazu.
Steigender Bedarf an effizienten Berechnungsverfahren
Technische Simulation findet oft in frühen Phasen der Produktentwicklung Anwendung, um mit schnellen Vorhersagen Designentscheidungen zu erleichtern. Aufgrund von Wechselwirkungen zwischen Bauteilen und Umgebungen sollen möglichst Gesamtsysteme durch Simulationen abgebildet werden. In der Strukturmechanik steigt die Größe der Simulation beispielsweise durch geometrisch komplexe Bauteile, kleinskalige Strukturen in großen Verbundbauteilen oder Kontakt- und Dynamiksimulationen. Folglich steigt der Bedarf an effizienten und leistungsfähigen Berechnungsverfahren weiter. Moderne Rechner erreichen höhere Leistungen unter anderem durch Mehrkern-CPUs, welche Berechnungen parallel ausführen können. Es gilt also, Finite-Elemente-Simulationen für die Ausführung auf solchen Rechnern anzupassen.
Idee der Gebietszerlegung
Um Finite-Elemente-Simulationen für parallele Berechnungen anzupassen, liegt eine Zerlegung des Berechnungsgebiets bzw. der Struktur nahe. Die Substrukturen werden jeweils für sich auf einem Rechenkern gelöst.
An einem dieser Substrukturierungs-Verfahren, der FETI (Finite Element Tearing and Interconnecting) Methode, wird am Lehrstuhl für Angewandte Mechanik der Technischen Universität München geforscht.
Wie funktioniert FETI?
Durch die Substrukturierung entstehen Schnittflächen mit Schnittkräften, wie in Abbildung 1 zu sehen ist. Diese Schnittkräfte sind für die Kommunikation zwischen den Substrukturen und damit den Rechenkernen zuständig und werden mit einem iterativen Gleichungslöser so gelöst, dass keine Lücken zwischen den Substrukturen auftreten.
Die Verschiebungen infolge der Schnittkräfte werden mit einem direkten Gleichungslöser auf jeder Substruktur separat berechnet. Einige Substrukturen schweben jedoch aufgrund fehlender Verschiebungs-Randbedingungen frei im Raum. Dies führt zu nicht eindeutig lösbaren Gleichungssystemen.
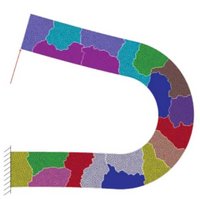
Bei FETI wird diesem Problem begegnet, indem die Verschiebungen in Starrkörperbewegungen und innere Deformationen aufgeteilt werden. Die Starrkörpermoden werden dann so gewählt, dass die deformierten Substrukturen ohne Lücken an den richtigen Positionen liegen. So kann eine eingespannte Struktur unter Last, wie in Abbildung 2, berechnet werden. Die eingefärbten Bereiche stellen einzelne Substrukturen dar.
Vor- und Nachteile des Verfahrens
Das FETI-Verfahren zeichnet sich durch seine Robustheit und Skalierbarkeit aus. Für parallele Algorithmen ist die Skalierbarkeit ein wichtiges Kriterium zur Beurteilung ihrer Leistungsfähigkeit. Darunter versteht man die Abnahme der Rechenzeit mit zunehmender Anzahl an Rechenkernen. So ist mit FETI die effiziente Lösung von Problemen mit mehreren Milliarden Freiheitsgraden auf mehreren hunderttausend Rechenkernen möglich.
Direkte Lösungsverfahren werden für derart große Probleme durch großen Speicherbedarf und Rechenaufwand ineffizient. Bei FETI ist jedoch ein erhöhter Grundaufwand nötig, weshalb der Einsatz erst bei großen Systemen interessant wird.
Aktuelle Problemstellungen und Forschungsthemen
Das lineare FETI-Verfahren zur Lösung statischer Probleme hat sich durch hohe Effizienz und Robustheit bewährt. Dynamische Strukturen wurden jedoch bislang wenig behandelt und sind Gegenstand der Forschung. Besonders heterogene Strukturen, also Substrukturen mit sehr unterschiedlichen Steifigkeiten, behindern die Konvergenz des Verfahrens.

Heterogene Strukturen treten beispielsweise bei Faserverbundwerkstoffen oder Autoreifen mit eingearbeitetem Stahlgewebe auf. Neben der linearen Dynamik wird aktuell an der Anwendung von FETI für nichtlineare Dynamik geforscht. Nichtlinearitäten können durch große Deformation, nichtlineares Materialverhalten wie bei Gummi, oder plastische Verformungen hervorgerufen werden. Effiziente nichtlineare Berechnungsverfahren sind also für die praktische Anwendung besonders relevant und bieten noch vielfältige Forschungsmöglichkeiten.
Erstmals erschienen in: TiB Ausgabe 2017 September/Oktober
